Josephson Junction Model (RSJ Modxel)

The parameters marked with an asterisk in the area column scale with the ics parameter given in the device line, not necessarily linearly. The present model paradigm assumes that the model parameters apply to a ``reference'' junction, which is a typical mid-critical current device as produced by the fouhdry. Instantiations derive from the reference device for a desired critical current. Appropriate scaling, not necessarily linear, will be applied when formulating instance capacitance and conductances.

Josephson Junction RSJ Model (levels 1 and 2) Parameters

JJ Model Parameters
name	area	parameter	units	default
level		Model type	-	1
pijj		Default is a pi junction	-	0
rtype		Quasiparticle current model	-	1
cct		Critical current model	-	1
icon		Critical current first zero	A	1.0e-2
tc		Superconducting transition temperature	K	9.26
tdebye		Debye temperature	K	276
tnom		Parameter measurement temperature	K	4.2
deftemp		Operating temperature	K	tnom
tcfct		Temperature dependence fitting parameter		1.74
vg or vgap		Gap voltage	V	2.6e-3
delv		Gap voltage spread	V	80.0e-6
icrit	*	Reference junction critical current	A	1.0e-3
cap	*	Reference junction capacitance	F	0.7e-12
cpic		Capacitance per critical current	F/A	0.7e-9
cmu		Capacitance scaling parameter		0.0
vm		Reference junction icrit*rsub	V	16.5e-3
rsub or r0	*	Reference junction subgap resistance	$\Omega$	vm/icrit
icrn		Reference junction icrit*rnorm	V	1.65e-3
rnorm or rn	*	Reference normal state resistance	$\Omega$	icrn/icrit
gmu		Conductance scaling parameter		0.0
icfct or icfact		Ratio of critical to step currents	-	$\pi$/4
force		no limits imposed on vm, rsub, icrn, rnorm		0
vshunt		Voltage to specify external shunt resistance	V	0.0
lsh0		Shunt resistor inductance constant part	H	0.0
lsh1		Shunt resistor inductance per ohm	H/$\Omega$	0.0
tsfactor		Phase change max per time step per 2$\pi$		$\tt dphimax$/2$\pi$
tsaccel		Ratio max time step to that at <tt>vdp</tt>		1.0
vdp		Dropback voltage (read only)

Detailed information about these parameters is presented below. Unless stated otherwise, this information also applies to the internal RSJ model (level=1) and the Verilog-A Josephson junction model provided with WRspice in the Verilog-A examples (level=2).

level
This specifies the model to use. There are three choices provided in WRspice. Level 1 (the default) is the internal RSJ model, and level 2 indicates the Verilog-A example RSJ model, which is available if it has been loaded. The third choice is level 3, which is an internal microscopic tunnel junction model described in the next section.

pijj
If this flag is given a nonzero integer value, the junctions will be modeled as a ``pi junction'' meaning that the zero-current phase is 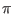$\pi$ rather than zero. Such devices have been fabricated using ferromagnetic barrier materials. Although these devices have some interesting behavior, they are not at this point available or used with any frequency.

rtype
The rtype parameter determines the type of quasiparticle branch modeling employed. Legal values are listed below, only 0 and 1 are supported in level 2.

0	The junction is completely unshunted, all shunt conductances set to zero.
1	Standard model (the default).
2	Analytic exponentially-derived approximation.
3	Fifth order polynomial expansion model.
4	``Temperature'' variation, allow modulation of the gap parameter.

Values for rtype larger than 1 are not currently supported in the Verilog-A model supplied with WRspice in the Verilog-A examples.

The default is rtype=1. Setting rtype=0 will disable modeling of the quasiparticle current, effectively setting the shunt resistance to infinity. Conditions with rtype=1 and 2 are as described by Jewett, however it is not assumed that the normal resistance projects through the origin. The icfact parameter can be set to a value lower than the default BCS theoretical value to reflect the behavior of most real junctions. The quasiparticle resistance is approximated with a fifth order polynomial if rtype=3, which seems to give good results for the modeling of some NbN junctions (which tend to have gently sloping quasiparticle curves).

Rtype=4 uses a piecewise-linear quasiparticle characteristic identical to rtype=1, however the gap voltage and critical current are now proportional to the absolute value of the control current set with a control=src_name entry in the device line. This is to facilitate modeling of temperature changes or nonequilibrium effects. For control current of 1 (Amp) or greater, the full gap and critical current are used, otherwise they decrease linearly to zero. If no device control source is specified, the algorithm reverts to rtype=1. It is expected that a nonlinear transfer function will be implemented with a controlled source, which will in turn provide the controlling current to the junction in this mode. For example, the controlling current can be translated from a circuit voltage representing temperature with an external nonlinear source. The functional dependence is in general a complicated function, but a reasonable approximation is 1 - (T/T_c)⁴ . See the examples (A.5) for an example input file (ex10.cir) which illustrates rtype=4.

It is currently not possible to use other than the piecewise linear model with this type of temperature variation. If rtype=4, then legal values for the critical current parameter are cct=0 (no critical current) and cct=1 (fixed critical current). If another value is specified for cct, cct reverts to 0. Thus, magnetic coupling and quasiparticle injection are not simultaneously available.

cct
The cct parameter can take one of the following values in level 1, only 0 and 1 are supported in level 2.

0	No critical current.
1	Fixed critical current.
2	Sin(x)/x modulated supercurrent.
3	Symmetric linear reduction modulation.
4	Asymmetric linear reduction modulation.

Values for cct larger than 1 are not currently supported in the Verilog-A model supplied with WRspice in the Verilog-A examples.

The control instance parameter should be used with devices using cct 2,3, or 4. With cct=2, the first zero is equal to the value of the model parameter icon. For cct=3, the maximum critical current is at control current zero, and it reduces linearly to zero at control current = 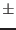$\pm$icon . Junctions with cct=4 have maximum critical current at control current = - icon, and linear reduction to zero at control current = + icon. If cct is specified as 2, 3, or 4, the area parameter, if given, is set to unity. Otherwise, the model parameters are scaled appropriately by the area before use.

icon
range: 1e-4 - 1.0
Level 1 only.
This parameter applies when the cct parameter is set to one of the choices larger the 1, where critical current modulation is modeled. The value of icon is the first value for (assumed) full suppression of critical current.

The parameter is not currently recognized by the Verilog-A Josephson junction model provided with WRspice, as that model does not currently support values of cct larger than 1.

tc
range: 0.1K - 280K
This is the transition temperature of the material used in the Josephson junction. We assume that both junction electrodes use the same material. The default value is 9.26K, the transition temperature of niobium.

tdebye
range: 40K - 500K
This is the Debye temperature of the material used in the Josephson junction. The default is 276K corresponding to niobium. The model support can compute the superconducting energy gap as a function of temperature, transition temperature, and Debye temperature using a BCS expression.

tnom
range: 0.0K - 0.95*tc
This is the temperature at which all model parameters are measured. The default is 4.2K, the boiling point of liquid helium.

deftemp
range: 0.0K - 0.95*tc
This is the default operating temperature of instances of the model, which can be overridden on a per-instance basis by specifying the temp_k instance parameter. The default is the tnom value.

tcfct
range: 1.5 - 2.5
This is an empirical fitting parameter for approximate temperature dependence (see 2.17.2.2) of the energy gap, default is 1.74.

icrit
range: 1nA - 0.1A
This is the critical current of the reference junction at nominal temperature, which defaults to 1.0mA if not given. This parameter is not used if cct is 0. the superconducting current through a Josepjson junctions is

I = I_csin(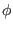$\phi$)

where I_c is the critical current. and the junction ``phase'' is

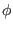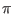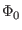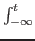$\phi$ = (2$\pi$/$\Phi_{0}^{}$)$\int^{t}_{{-\infty}}$V(t)dt .

The V(t) is the junction voltage, and 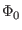$\Phi_{0}^{}$ is the magnetic flux quantum.

The icrit parameter should not be confused with the ics instance parameter. The latter is actually a scale factor which specifies the instantiated device critical current as well as appropriately scaling conductances and capacitance, from the model reference current which is icrit.

vg or vgap
range: 0.1mV - 10.0mV
This parameter specifies the gap voltage, which in a hysteretic Josephson junction is a voltage at which there is a large and abrupt increase in conductivity. This parameter is material dependent. If not given, the value used is computed using BCS theory from the operating temperature, superconducting transition temperature, and Debye temperature, assuming both electrodes are identical.

delv
range: 0.001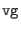$\tt vg$ - 0.2$\tt vg$
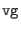
This specifies the assumed width, in voltage, of the quasiparticle step region, or gap. In this region, current increases sharply with increasing voltage. The default value of 80uV is reasonable for high-quality niobium/aluminum oxide Josephson junctions independent of foundry.

cap
range: 0.0 - 1nF
This is the capacitance of the reference junction, in farads. This will override the cpic parameter if given, setting a fixed value for reference junction capacitance, invariant with icrit. If not given, junction specific capacitance is set via the cpic parameter, see below.

cpic
range: 0.0 - 1e-9
This supplies the default capacitance per critical current in F/A. This defaults to the MIT Lincoln Laboratory SFQ5EE process <a href="tolpygo">[Tolpygo]</a> value (0.7pF for 1.0 mA), and will set the junction capacitance if <tt>cap</tt> is not given. With <tt>cap</tt> not given, changing <tt>icrit</tt> will change the assumed capacitance of the reference junction.

cmu
range: 0.0 - 1.0
This is a new parameter in the current model, which is intended to account for nonlinearity in scaling of capacitance with area (or critical current, we actually define ``area'' as the actual over the reference critical current). It is anticipated that the actual junction capacitance consists of two components: a physical area dependent ``bulk'' term, and a perimeter-dependent fringing term. The cmu is a real number between 0 and 1 where if 0 we assume no perimeter dependence, and if 1 we assume that all variation scales with the perimeter. The default value is 0. The capacitance of an instantiated junctions is as follows:

C = cap(A(1 - cmu) + 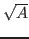$\sqrt{{A}}$cmu)

Here, A is the ``area'' scaling factor, which is the ratio of the junction critical current to the reference critical current.

vm
range: 8mV - 100mV
This is the product of the reference subgap resistance and the reference device critical current. This parameter is commonly provided by foundries, and is a standard indicator for junction quality (higher is better). Values tend to decrease with increasing critical current density. This defaults to the value for the MIT Lincoln Laboratory SFQ5EE process[16], which is 16.5mV, The reference junction subgap resistance is obtained from the value of this parameter and the critical current, unless given explicitly.

rsub or r0
range: 8mV/icrit - 100mV/icrit
The reference junction subgap resistance can be given directly with this parameter, and a given value will override the vm value if also given.

icrn
range: 1.5mV - 1.9mV
This is the product of the reference junction ``normal state'' resistance and the critical current, where the normal state resistance is the differential resistance measured well above the gap. The default value is that provided for the MIT Lincoln Laboratory SFQ5EE process[16] which is 1.65mV. This too is a commonly given parameter from Josephson foundries for characterizing junctions. If not specified explicitly, this provides the reference junction normal state resistance from the critical current.

rnorm or rn
range: 1.5mV/icrit - 1.9mV/icrit
The reference junction normal state resistance can be given explicitly with this parameter, which will override icrn if this is also given.

gmu
range: 0.0 - 1.0
This is analogous to cmu, and applies to the subgap and normal conductances. The vm, in particular, may vary with junction physical size, with small junctions having lower vm than larger ones. This parameter should capture this effect. It is taken that a significant part of the conductivity is due to defects or imperfections around the periphery of the junction area, and the contribution would therefor scale with the perimeter. The scaling for conductivity is as follows:

G_x = G_x0(A(1 - gmu) + 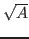$\sqrt{{A}}$gmu)

Here, G_x refers to either the subgap or normal conductance, G_x0 is the same parameter for the reference junction. The A is the scaling parameter, that is, the ratio of instance to reference critical currents. The default value is 0, meaning that scaling is assumed purely linear, which will be the case until a number is provided through additional data analysis. It may prove necessary to have separate scaling parameters for subgap and above gap condutance, at which time a new model parameter may be added.

icfct or icfact
range: 0.5 - 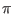$\pi$/4
This parameter sets the ratio of the critical current to the quasiparticle step height. Theory provides the default value of 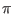$\pi$/4 which is usually adequately close. Characterization of fabricated junctions would provide an improved number.

force
range: 0 or 1
If this flag is set, then the only range test applied to subgap and above gap resistance values is that they be larger than zero. This affects the parameters that set the quasiparticle branch conductance values, any input other than a short circuit is allowed.

vshunt
range: 0.0 - nominal gap voltage
This parameter is unique in that it does not describe an as-fabricated junction characteristic. Rather, it is for convenience in specifying a shunt resistance to use globally in SFQ circuits, If given (in volts) conductance will be added automatically so that the product of the total subgap conductance and the critical current will equal vshunt. This avoids having to calculate the value of and add an explicit resistor across each Josephson junction, as used for damping in these circuits. The designer should choose a value consistent with the process parameters and the amount of damping required. Higher values will provide less damping, usually critical damping is desired. This parameter defaults to 0, meaning that no additional demping is supplied by default.

lsh0
range: 0.0 - 2.0pH

lsh1
range: 0.0 - 10.0pH/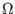$\Omega$
These parameters specify series parasitic inductance in the external shunt resistor. the vshunt parameter must be given a value such that the added external conductance is positive, or these parameters are ignored. The inductance consists of a constant part (lsh0) assumed to come from resistor contacts, plus a value (lsh1) proportional to the resistance in ohms, intended to capture the length dependence.

tsfactor
range: 0.001 - 1.0
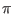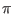This is mainly for compatibility with the Verilog-A Josephson junction model provided with WRspice in the Verilog-A examples. This is equivalent to the WRspice dphimax parameter, but is normalized to 2$\pi$ . If not given, it defaults to $\tt dphimax$/2$\pi$ in WRspice, or 0.1 in the Verilog-A model not used in WRspice. This is the maximum phase change allowed between internal time points.

tsaccel
range: 1.0 - 100.0
Time step limiting is performed relative to the Josephson frequency of the instantaneous absolute junction voltage or the dropback voltage, whichever is larger. The phase change is limited by tsfactor, thus corresponding to a maximum time step relative to the period of the frequency corresponding to the voltage. Note that in SFQ circuits, where the junctions are critically damped, the junction voltage is unlikely to exceed the dropback voltage, which is numerically equal to the critical current times the shunt resistance (vshunt). This implies that the maximum time step is a fixed value by default.

When simulating SFQ circuits, between SFQ pulses there is often significant time where signals are quiescent and one could probably take larger time steps, speeding simulation. This appears true to an extent, however one can see signs of instability if steps are too large.

The tsaccel parameter is the ratio of the longest time step allowed to that allowed at the dropback voltage. In computing the time step, the low voltage threshold is reduced to the dropback voltage divided by tsaccel, so time steps will be inversely proportional to voltages above this value.

Experimentation suggests that a value of 2.5 is a good choice for RSFQ circuits, your results may vary.

vdp (read only)
This parameter returns the computed value of the dropback voltage, which is the voltage at which the return trace of a hysteretic Josephson junction i-v curve snaps back to the zero-voltage state. If is also the voltage equivalent of the plasma resonance, and the product of critical current and shunt resistance for critical damping.