| JJ Model Parameters |
| name |
area |
parameter |
units |
default |
|---|
| level |
|
Model type |
- |
3 |
| coeffset |
|
Coefficient set name |
- |
|
| rtype |
|
Quasiparticle current enabled |
- |
1 |
| cct |
|
Critical current enabled |
- |
1 |
| tnom |
|
Parameter measurement temperature |
K
|
4.2 |
| deftemp |
|
Operating temperature |
K
|
tnom |
| tc |
|
Superconducting transition temperature |
K
|
9.26 |
| tc1 |
|
Superconducting transition temp side 1 |
K
|
9.26 |
| tc2 |
|
Superconducting transition temp side 2 |
K
|
9.26 |
| tdebye |
|
Debye temperature |
K
|
276 |
| tdebye1 |
|
Debye temperature side 1 |
K
|
276 |
| tdebye2 |
|
Debye temperature side 2 |
K
|
276 |
| smf |
|
Riedel smoothing factor |
-
|
0.008 |
| nterms |
|
Terms in fit table |
-
|
8 |
| nxpts |
|
Points in TCA table |
-
|
500 |
| thr |
|
Fitting threshold parameter |
-
|
0,2 |
| icrit |
*
|
Reference junction critical current |
A
|
1.0e-3 |
| cap |
*
|
Reference junction capacitance |
F
|
0.7e-12 |
| cpic |
|
Capacitance per critical current |
F/A
|
0.7e-9 |
| cmu |
|
Capacitance scaling parameter |
|
0.0 |
| vm |
|
Reference junction icrit*rsub |
V
|
16.5e-3 |
| rsub or r0 |
*
|
Reference junction subgap resistance |
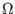
|
vm/icrit |
| gmu |
|
Conductance scaling parameter |
|
0.0 |
| icfct or icfact |
|
Ratio of critical to step currents |
- |
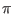 /4 /4
|
| force |
|
no limits imposed on vm, rsub |
|
0 |
| vshunt |
|
Voltage to specify external shunt resistance |
V
|
0.0 |
| lsh0 |
|
Shunt resistor inductance constant part |
H
|
0.0 |
| lsh1 |
|
Shunt resistor inductance per ohm |
H/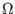
|
0.0 |
| tsfactor |
|
Phase change max per time step per 2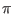
|
|
 /2 /2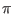
|
| tsaccel |
|
Ratio max time step to that at <tt>vdp</tt> |
|
1.0 |
| del1 (read only) |
|
Energy gap side 1 |
V
|
|
| del2 (read only) |
|
Energy gap side 2 |
V
|
|
| vg or vgap (read only) |
|
Gap voltage |
V
|
|